Bapat–Beg theorem
In probability theory, the Bapat–Beg theorem[1] gives the joint cumulative distribution function of order statistics of independent but not necessarily identically distributed random variables in terms of the cumulative distribution functions of the random variables. A simple proof of this can be found in [2]
Ordinarily, all elements of the sample are obtained from the same population and thus have the same probability distribution. The Bapat–Beg theorem describes the order statistics when each element of the sample is obtained from a possibly different population with a different probability distribution.
Contents |
The theorem
Let 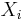 ,
, 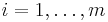 be independent real valued random variables with cumulative distribution functions
be independent real valued random variables with cumulative distribution functions 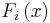 . Denote the order statistics by
. Denote the order statistics by 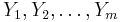 , with
, with 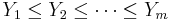 . Further let
. Further let 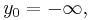
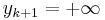 , and
, and
for all 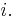 For
For 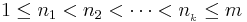 and
and 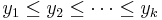 , the joint cumulative distribution function of the subset
, the joint cumulative distribution function of the subset  of the order statistics satisfies
of the order statistics satisfies
where
is the permanent of a block matrix with the subscript 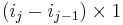 denoting the dimension of a block obtained by repeating the same entry, and the block row index
denoting the dimension of a block obtained by repeating the same entry, and the block row index 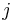 and block column index
and block column index 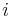 .
.
The independent identically distributed case
In the case when the variables 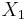 ,
,  are independent and identically distributed with cumulative probability distribution function
are independent and identically distributed with cumulative probability distribution function 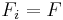 for all
for all 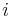 , the Bapat–Beg theorem reduces to [3]
, the Bapat–Beg theorem reduces to [3]
where again
Remarks
- No assumption of continuity of the cumulative distribution functions is needed.
- The theorem is formulated for the joint cumulative probability distribution function in terms of a subset of the order statistics and ordered arguments. If the inequalities
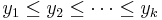 are not imposed, some of the inequalities
are not imposed, some of the inequalities 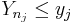 may be redundant (because always
may be redundant (because always 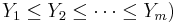 and the argument list needs to be first reduced by dropping all
and the argument list needs to be first reduced by dropping all 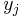 such that
such that 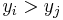 for some
for some 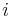 .
.
Complexity
The Bapat–Beg formula involves exponentially many permanents, and the complexity of the computation of the permanent itself is at least exponential (unless P = NP). Thus, in the general case, the formula is not practical. However, when the random variables have only two possible distributions, the complexity can be reduced to 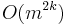 .[3] Thus, in the case of two populations, the complexity is polynomial in m for any fixed number of statistics k.
.[3] Thus, in the case of two populations, the complexity is polynomial in m for any fixed number of statistics k.
See also
- For standard results for the distribution of order statistics for independent and identically-distributed random variables see, for example,[4]
- permanent
- independent and identically-distributed random variables
Notes
- ^ R. B. Bapat and M. I. Beg. Order statistics for nonidentically distributed variables and permanents. Sankhyā Ser. A, 51(1):79–93, 1989. MR1065561
- ^ Sayaji Hande. A note on order statistics for nonidentically distributed variables Sankhyā Ser. A, 56(2):365–368, 1994. MR1664921
- ^ a b Glueck; Anis Karimpour-Fard; Jan Mandel; Larry Hunter; Muller (2008). "Fast computation by block permanents of cumulative distribution functions of order statistics from several populations". Communications in Statistics - Theory and Methods 37 (18): 2815–2824. arXiv:0705.3851. doi:10.1080/03610920802001896. PMC 2768298. PMID 19865590. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=2768298.
- ^ N. Balakrishnan and C. R. Rao. Order statistics: an introduction. In Order statistics: theory & methods, volume 16 of Handbook of Statist., pages 3–24. North-Holland, Amsterdam, 1998.
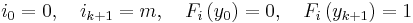
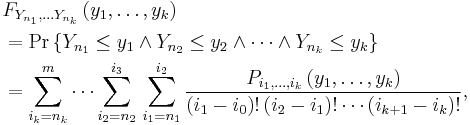
![\begin{align} & P_{i_{1},\ldots,i_{k}}\left( y_{1},\ldots,y_{k}\right) \\ & \quad=\text{per}\begin{bmatrix} \left[ F_{i}(y_{j})-F_{i}(y_{j-1})\right] _{\left( i_{j}-i_{j-1}\right) \times1}\end{bmatrix} _{j=1,i=1}^{j=k%2B1,i=m}\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/7c07e62780d913cf099967a76a60e2b4.png)
![\begin{align} & F_{Y_{n_{1}},\ldots Y_{n_{k}}}\left( y_{1},\ldots,y_{k}\right) \\
& =\Pr\left\{ Y_{n_{1}}\leq y_{1}\wedge Y_{n_{2}}\leq y_{2}\wedge \cdots\wedge Y_{n_{k}}\leq y_{k}\right\} \\ & =\sum_{i_{k}=n_{k}}^{m}\cdots\sum_{i_{2}=n_{2}}^{i_{3}}\,\sum_{i_{1}=n_{1}}^{i_{2}}m!\prod\limits_{j=1}^{k%2B1}\frac{\left[ F\left( y_{j}\right) -F\left( y_{j-1}\right) \right] ^{i_{j}-i_{j-1}}}{\left( i_{j}-i_{j-1}\right) �!}, \end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/546cfff2e4fc656a35a18a6bffc9f858.png)